某些数据结构似乎在图形应用程序中反复出现,可能是因为它们涉及基本的底层思想,例如表面、空间和场景结构。本章讨论几个基本且不相关的数据结构类别,它们是最常见和最有用的:网格结构、空间数据结构、场景图和分块多维数组。
对于网格,我们讨论了用于存储静态网格和将网格传输到图形 API 的基本存储方案。我们还讨论了翼边数据结构 (wingededge data structure)(Baumgart, 1974) 和相关的半边结构(half-edge structure),这对于管理细分变化的模型很有用,例如在细分或模型简化中。虽然这些方法可以推广到任意多边形网格,但我们在这里关注更简单的三角形网格。
接下来介绍场景图(scene graphs)数据结构。这种数据结构的各种形式在图形应用程序中无处不在,因为它们在管理对象和转换方面非常有用。所有新的图形 API 都旨在很好地支持场景图。
对于空间数据结构,我们讨论了在 3D 空间中组织模型的三种方法——包围体层次结构(bounding volume hierarchies)、层次空间细分(hierarchical space subdivision)和均匀空间细分(uniform space subdivision)——以及使用层次空间细分(BSP 树)去除隐藏表面。同样的方法也用于其他目的,包括几何剔除和碰撞检测。
最后,给出了分块多维数组。最初开发是为了帮助需要从磁盘换入图形数据的应用程序中的分页性能,这种结构现在对于机器上的内存位置至关重要,无论数组是否位于主存。
大多数现实世界的模型都是由具有共享顶点的三角形复合体组成的。这些通常称为三角形网格或不规则三角形网络 (TINs),有效地处理它们对于许多图形程序的性能至关重要。哪种效率很重要取决于应用。网格存储在磁盘和内存中,我们希望尽量减少消耗的存储量。当网格通过网络或从 CPU 传输到图形系统时,它们会消耗带宽,这通常比存储更宝贵。在对网格执行操作的应用程序中,除了简单地存储和绘制它们(例如细分、网格编辑、网格压缩或其他操作)之外,对邻接信息的有效访问至关重要。
三角形网格通常用于表示曲面,因此网格不仅仅是不相关三角形的集合,而是通过共享顶点和边相互连接以形成单个连续曲面的三角形网络。这是关于网格的一个关键见解:处理网格比处理相同数量的不相关三角形的集合更有效。
三角形网格所需的最少信息是一组三角形(顶点的三元组)及其顶点的位置(在 3D 空间中)。但是很多程序需要能够在顶点、边或面上存储额外的数据以支持纹理映射、着色、动画和其他操作。顶点数据是最常见的:每个顶点都可以有材质参数、纹理坐标和辐照度(irradiances)——任何其值在表面上发生变化的参数。然后将这些参数线性插值到每个三角形上,以定义整个网格表面上的连续函数。然而,能够按边或按面存储数据有时也很重要。
网格类似于表面的想法可以形式化为对网格拓扑的约束——三角形连接在一起的方式,而不考虑顶点位置。许多算法只能在具有可预测连接性的网格上工作,或者更容易实现。对网格拓扑结构的最简单和最严格的要求是表面是流形。流形网格是“水密的”——它没有缝隙,将表面内部的空间与外部的空间隔开。它看起来也像网格上各处的一个表面。
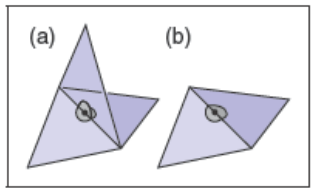
术语流形来自拓扑学的数学领域:粗略地说,流形(具体来说是二维流形,或2-流形)是一种表面,其中任何一点周围的一个小的邻域都可以被平滑成一个小的平面。这个想法可以通过反例得到最清楚的解释:如果网格上的一条边有三个三角形连接到它,那么边缘上一个点的邻域与其中一个三角形内部一个点的邻域是不同的,因为它有一个额外的“鳍”伸出来,如果边缘上有两个三角形,边缘上的点就像内部的点一样有邻域,只是中间有一条折痕:

类似地,如果共享一个顶点的三角形处于下图左侧的配置,则邻域就像在中心粘在一起的两块表面。下图右边所示的具有简单邻域的顶点就可以了:
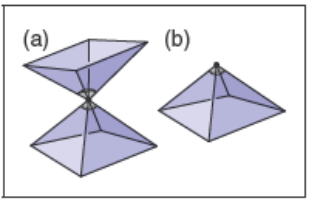
许多算法假设网格是流形的,如果输入一个畸形的网格,验证这个属性以防止崩溃和无限循环,总是一个好主意。验证这个可以归结为检查所有的边都是流形的,并通过验证以下条件检查所有的顶点都是流形的:
(1)每条边都只由两个三角形共用
(2)每个顶点周围都有一个简单、完整的三角形循环顺序