在图形学中,我们经常需要处理连续变量的函数,比如自然界中的图像。但是连续往往意味着无穷,在有穷的计算机存储的条件下,我们必须将这种连续函数表示为有穷位数的集合,也就是离散的。我们通常通过**采样(sample)**的方法,捕捉连续函数中足够多的点,存储这些点的值,并把这些值的集合代表这个连续函数。在我们需要的时候,我们还可以通过这些点重建出当初未采样位置的点的值(比如插值),进而更加完整地还原出连续函数的面貌(当然相对于真正的连续函数,这只是一种近似)。
比如相机拍摄自然界图像的时候,就是一种采样。相机将2D图像平面上连续的色彩变化记录为二维的网格值(grid value)。这就将原始的连续函数$ℝ^2 ↦ C$转变为了离散函数$ℤ^2 ↦ C$。还有像平板电脑的手写笔书写,也是将手写笔在屏幕上的连续运动$ℝ ↦ ℝ^2$转变为不同时间戳下手写笔所处屏幕位置的序列集合$ℤ ↦ ℝ^2$。运动捕捉系统也是同样的道理,只不过是记录三维的位置信息:$ℝ ↦ ℝ^3$变为$ℝ ↦ ℝ^3$。医学CT装置要记录人体不同位置的密度信息,是将连续的3D位置转变为微小的体素网格:$ℝ^3 ↦ ℝ$变为$ℤ^3 ↦ ℝ$。
从上述这些例子可以看到,很多地方都需要用到采样这样的技巧:
In all cases, a function is being sampled at the points of a lattice in one or more dimensions, and in all cases, we need to be able to reconstruct that original continuous function from the array of samples.
可能有人会觉得如果采样的点足够多,我们就可以完全用采样去取代连续函数,但这是错误的。因为从采样的定义来说,我们永远只是得到了一个近似。对于图像来说,放大和缩小它就会导致aliasing。明白aliasing如何产生,以及明白如何预防aliasing的产生,就需要知道采样的数学原理。

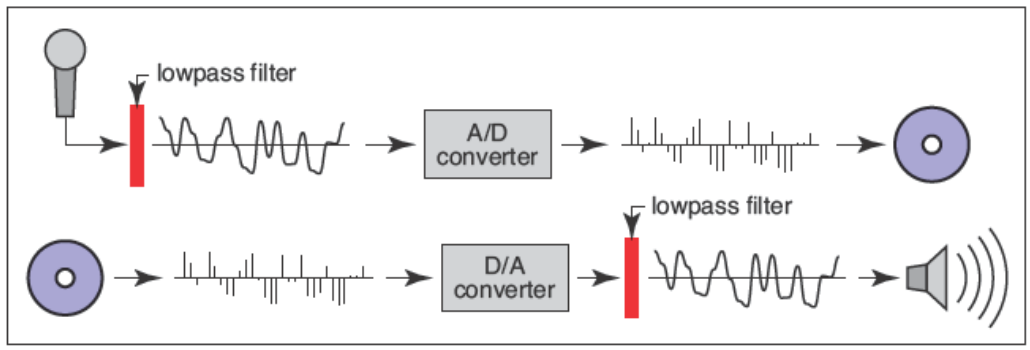
上图是音频记录和重现的全过程。
音频接收器将音波送到模数转换器(A/D or ADC),ADC以每秒几千次的采样频率将其转换为离散的电压信号(这是一个值),送入到存储器。
当需要播放声音时,存储器将离散的电压信号取出,送入到数模转换器(D/A or DAC),产生相应的电压,电压会使得发声单元的鼓膜产生相应的移动,进而复现声音。
“每秒几千次的采样频率”被称为采样率,采样率的高低取决于想要录制的声音的高频程度。比如想要录制短笛的声音,一个低频的采样频率就会导致奇怪的结果,而高频的采样率就可以很好地记录并再现。为了避免因采样不足造成的问题,音频接收器会对ADC的输入进行低通过滤,以去除可能导致问题的高频。
在输出方面会有同样的问题。DAC产生的电压只会在新样本进入时变化,而在下一个样本进入之前都会保持稳定。这就导致DAC输出的电压曲线实际是一种阶梯状的,这种阶梯意味着一种高频,依赖于采样率的,一种嗡嗡的声音。为了消除这种高频,DAC的输出通常也会经过低通滤波,降低高频,平滑电压曲线。
上述音频记录和重现的采样思想也被用于图形学相关领域中。采样不足(undersampling)的问题同样也会出现,而解决方法也是一致的:
filtering before sampling and filtering again during reconstruction.
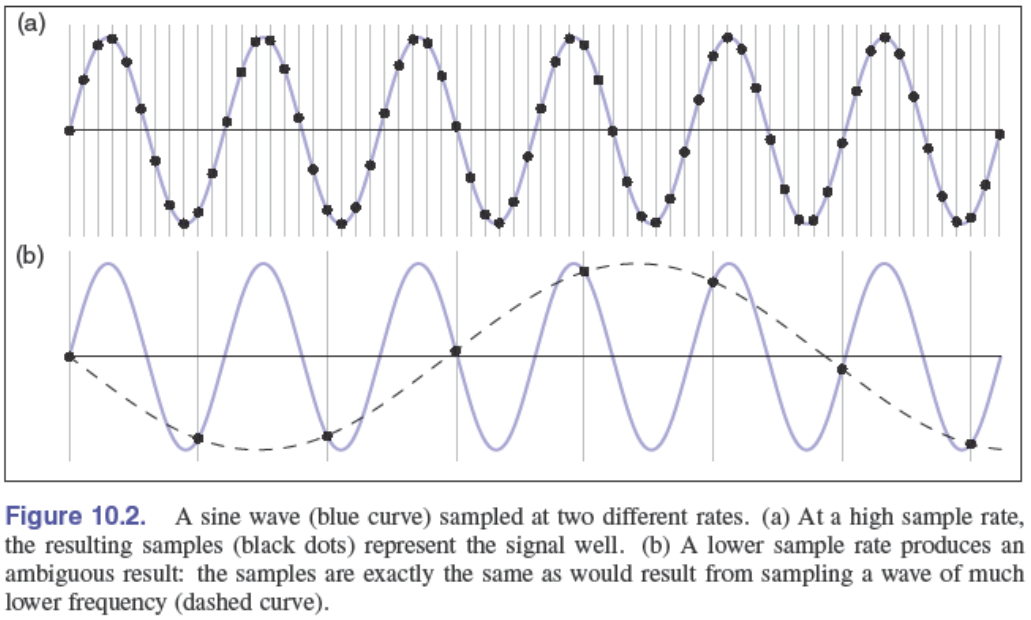
上述就是一个具体的例子。对于一个正弦波(sin),采用较高的采样率可以很好的表达原始信号,但是采用较低的采样率,就仿佛我们是在一个原始的低频信号上进行的采样。这两种不同频率的采样,它们得到的值都是正确的,但是却产生了仿佛是在不同频率的原始信号上进行采样的结果。假如我们采用了第二种采样方式,通过得到的采样值,我们无法分辨原始信号是(b)中采样值拟合出的低频信号还是(a)中的高频信号,而我们往往倾向于它是低频的。所以,如果对一个高频原始信号采用低频采样,高频原始信号就会伪装成低频信号,这种现象就叫做aliasing。
