无论是ray-tracing还是rasterization,实时或者批处理,一个很重要的任务就是针对3D场景中不同物体的形状和物体间的关系对它们进行着色。
在物理世界中,大部分的光是反射的光,而光的反射属性很大程度受到反射表面几何的影响。
针对不同的应用场景,会采用不同的shading目标,从而带来不同的视觉效果和性能消耗。
用来计算shading的公式被称为shading model。针对上述不同的应用场景会有不同的shading model。但是所有的shading model都必须包含基础的物理光反射估计。在这个基础上可以加入/修改/删除更多的功能使得shading更适用于不同的目标和风格。
shading model可以独立于其他的rendering system,同一个shading model可以分别用在ray-tracing和rasterization上。本章会介绍点光源-不透明表面的简单shading model,更多内容在第14章。
在现实世界中,表面接收到的光线来自四面八方。但在模型照明中,最简单的情况就是光线来自一个单一的方向。
这是一个理想化的情况,但是对于发光面积远小于光线到达物体的距离的光源来说,这很有用。
把这种光源抽象成点光源,可以有很多好处,我们可以不用关心光源的体积和几何信息,只需要知道它的位置和光线的方向。
正常的点光源一般是各向同性的,即往各个方向发出的光是一样的,有些聚光灯效果的点光源则不是这样。
对于一个点光源来说,需要知道它的位置和强度(有多少光穿过一个单位面积的表面)

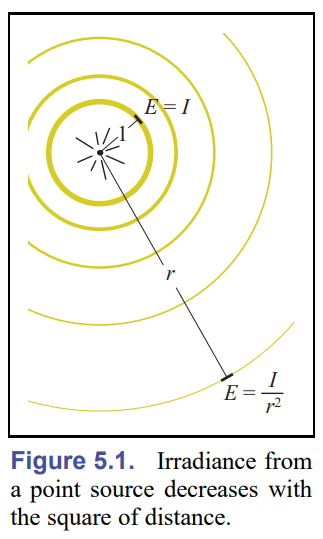
对于一个各向同性的点光源,我们想要知道距离点光源一段距离的单位表面会接受到多少强度的光。
假设点光源的power总共为1 watt,并且被放置在一个单位长度球体的中心。因为各向同性,点光源所有的power都会被打到球体的内壁,并且均匀分布。那么球体上单位面积接受到的power为:
$$
irradiance = \frac{P}{4\pi r^2} = \frac{P}{4\pi} $$
随着$r$不断改变,irradiance也会不断变化,且与$r^2$成反比,那么任意距离的irradiance为:
$$
irradiance-E = \frac{P}{4\pi}\frac{1}{r^2} = \frac{I}{r^2} $$