
当试图复制现实世界的外观时,人们很快就会意识到几乎没有任何表面是没有特征的。所有的材料放入现实世界后,必定会很快布满痕迹、凹痕、污渍、划痕、指纹和污垢。
在计算机图形学中,我们把这种现象称为“spatially varying”的表面属性,也就是这种表面属性因地而异,但并没有改变这个表面的真正的形状。为了实现这些效果,各种建模和渲染系统都提供了一些纹理映射的方法:使用一张图像,被称作texture map 或者 texture image。或者就只是一个texture,去存储想要在表面上实现的细节,然后使用数学的方法将图像或者纹理**映射(mapping)**到物体表面上。
事实证明,一旦将图像映射到物体表面的机制存在,纹理映射还能做远远不止创造表面细节的事情,比如创造阴影和反射、提供照明、甚至可以定义出物体的形状。在复杂的交互程序中,纹理被用来存储各种数据,这些数据甚至与图片无关!
本章讨论使用纹理来表示表面细节、阴影和反射。虽然基本思想很简单,但是一些实践性的问题会让纹理的使用复杂化。首先,纹理很容易变形,所以这种映射会很有挑战性。其次,texture映射是一个resample的过程,就像重新缩放图像一样,正如在上一章提到,resample会带来混叠的问题。纹理映射和动画的一起使用很容易会带来混叠的问题,所以大部分纹理系统之所以复杂就是为了antialiasing。
从简单的场景开始考虑——一个木质地板。我们希望用显示木地板木纹的图像控制地板的漫反射颜色。不管是光追还是光栅化(前者需要计算光线与物体交点的颜色,后者需要计算光栅化后的片段颜色),我们都需要知道在这个shading point上纹理的颜色,将其作为漫反射颜色,以便于使用第5章提到的Lambertian渲染模型。
为了得到这个颜色,着色器执行纹理查找:它在纹理图像的坐标系统中找出与shading point对应的location,并读取图像中该点的颜色,从而得到纹理样本。不同的像素对应图像中不同的位置,从而得到不同的颜色,代码如下:

在这段代码中,着色器要求物体表面中的shadepoint能够提供坐标给texture查询,并且希望每个使用这个texture的表面都能够给出这个坐标。这带来了纹理映射的第一个关键要素:需要一个从表面映射到纹理的函数,使得我们可以很容易计算出每个像素。这被叫做纹理坐标函数(texture coordinate function):
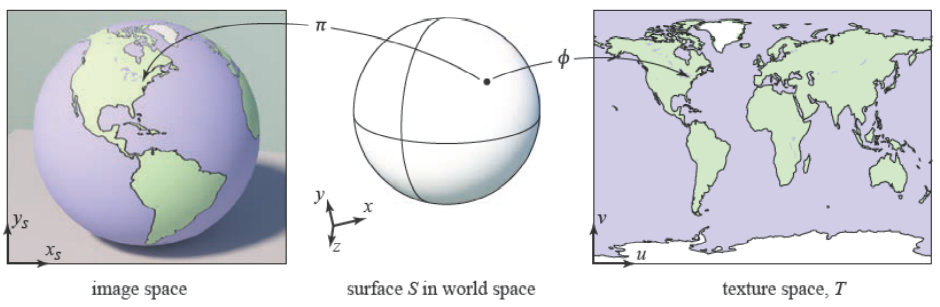
上图左侧部分是viewing projection的过程,是将S映射到图像上的任何一个位置(这时候还未光栅化),右侧是texture mapping的过程,是将S映射到纹理图上。
纹理坐标函数为物体表面上的每一个点都提供了纹理坐标。从数学角度,这是一个从3D域S到2D域T的映射:
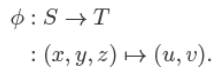
集合T,通常被叫做“纹理空间”,只是一个包含纹理图像的矩形。普遍地,我们会使用单位正方形$(u, v) ∈ [0, 1]^2$(在这本书中,我们使用u和v来表示纹理坐标)。这跟第8章提及的viewing projection(在本章被称作$π$过程)很相似,它将场景中的物体表面映射到了图像上的点。这两个过程都是3D to 2D的过程,也都是被渲染所需要的——一个需要知道怎么拿到纹理的值,一个需要知道怎么拿到图像像素的着色结果。但是这两个过程也有着重要的不同:$π$通常只包括投影变换和正交变换,而$ϕ$可以有很多不同的形式;$π$只需要在整个场景中执行一次,而对于场景中不同的物体,可能需要执行不同的$ϕ$。
有些人也许会感到惊讶,$ϕ$是一个从表面到纹理图像的映射,而我们最终的目标是将纹理“贴”到物体表面上,但这就是我们需要的函数。
对于上述木制地板的情况,如果地板的z值恒定,并且长宽与xy轴都对齐,那么我们就可以简单地使用下面的mapping:
$$ u = ax; v = by, $$
对于a、b的合适选择,可以为每个$(x, y, z)_{floor}$提供纹理坐标$(u, v)$,之后我们就可以使用纹理中位于这个位置的值,或者,texel(texture image中的pixel),即最接近$(u, v)$的像素值来作为$(x, y)$处的纹理值。最终我们可以得到下图: