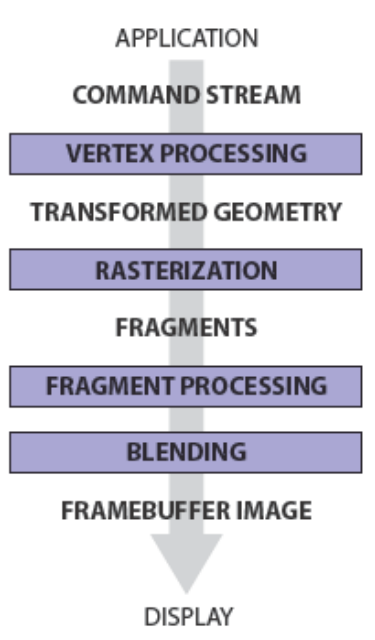
考虑object-order的渲染方式(rasterization),这对应着一系列操作,开始于objects,结束于更新图像上的像素。这些操作就被叫做Graphics Pipeline。
Object-order rendering在速度和效率上有着很大的优势。相比于反复检索被着色像素需要的场景物体,对场景物体中的每一位只需遍历一遍的方法显然快很多。
针对图形管线有两种类型,一种是用来做交互式渲染的api(OpenGL、Direct3D)的hardware pipelines,一种是用来做电影制作的api(RenderMan)的software pipelines。前者要求的是速度快,能够为游戏或者可视化提供快速的交互;后者要求的是图像质量高,要有华丽的视觉效果,还要支持大范围的场景,但是这需要大量的渲染时间。虽然两种管线的目的不同,但是有相当多的部分是相似甚至相同的。本章将关注这些共同的部分。
object-order rendering可以被分解为:(1)栅格化(2)栅格化前的坐标变换(3)栅格化后的像素操作。
对于(2),主要应用的是矩阵变换,前面几章已经做过介绍。对于(3),最常见的就是关于遮挡的z-Buffer。其他许多操作也可以用在不同阶段,从而实现各种各样的渲染效果(pipeline是一样的)。

图形管道可以分为上述四个阶段:(1)场景物体以顶点(vertex)的形式传入VERTEX PROCESSING,然后使用这些顶点的图元被传入RASTERIZATION。(2)RASTERIZATION将这些图元分为不同的片段(fragment,像素),一个片段对应一个图元包括的像素,片段将被送到FRAGMENT PROCESSING进行处理。(3)在FRAGMENT PROCESSING中,每个片段会被并行处理,并将处理结果送入BLENDING。(4)在BLENDING中,每个片段的处理结果将被组合。
本章将从栅格化开始,然后通过举例说明几何和像素阶段的目的。
栅格化和栅格器是任何图形管道的中心。对于传入的每一个图元,栅格器会执行两个操作:
(1)列举被图元覆盖的像素
(2)往图元里的像素插入“属性值”(由顶点属性值插值得到)
栅格器的输出是一堆片段,每一个片段对应被图元覆盖的一个像素,并且带着自己的一组属性值。
本章介绍栅格化主要是用来渲染3D场景,同样的方法也可以用来绘制2D图形。现在大部分2D图形的绘制也是利用3D图形系统。
对于给定两点屏幕坐标$(x0, y0)$和$(x1, y1)$,直线绘制命令需要绘制一些“reasonable”的像素来让直线看上去像直线。绘制这样的直线需要直线公式,而我们拥有两种直线公式——隐式的和参数化的。这节会介绍利用隐式直线表达的方法:
Line Drawing Using Implicit Line Equations
最常用的算法是midpoint algorithm(中点算法),该算法可以绘制出与Bresenham algorithm相同结果的线条,但是比其更加直接。
一条直线的隐式表达是:
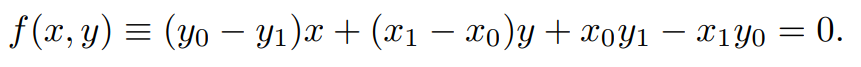
这里假设x0 ≤ x1,如果假设不成立就调换两点位置使其成立。那么斜率就可以表示为:
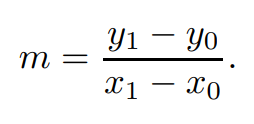
接下来的讨论都会要求$m ∈ (0, 1]$。类似的讨论可以延伸出$m∈( − ∞, − 1], m ∈( − 1, 0], m∈(1, ∞)$,这四种情况对应所有的可能。
对应$m∈(0, 1]$的情况,x变化的速度会比y快。在一些api中y轴的方向是朝下的,但这不影响算法(y轴朝上朝下算法的思想都是一致的),本章该算法的最终实现就是y轴朝下。
中点算法的核心假设就是我们会画一条尽可能瘦的线,使得连线之间没有断开(处于对角线位置的相邻像素不叫断开):
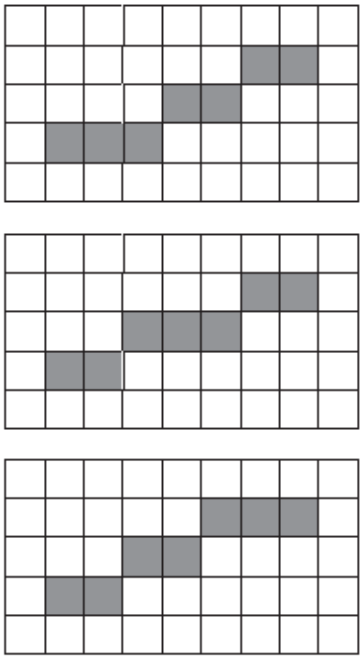
在绘制直线的过程中,只有两种可能:(1)绘制右边的像素(2)绘制上边的像素。所以我们只需要从左到右开始绘制直线,当满足某种条件时向右上走一格,不满足时向右走一格:
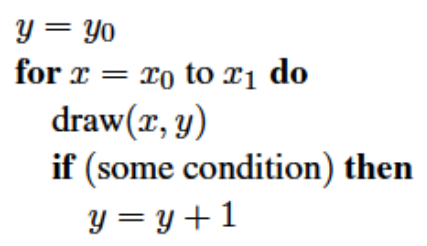
x,y都是整数。算法的关键就在于“某种条件”的制定。
keep drawing pixels from left to right and sometiones move upward in the y-direction while doing so.
可以通过中点去判断。假设我们当前绘制的点坐标是$(x, y)$,下一个需要绘制的候选点是$(x+1, y)$和$(x+1, y+1)$。因为坐标都是整数,但实际像素是一个单位正方形,它们以像素坐标为原点,上下左右扩充0.5长度。所以$(x+1, y)$和$(x+1, y+1)$两个像素的中点是$(x+1, y+0.5)$。如果直线在$x+1$位置的值大于$y+0.5$,则选择$(x+1, y+1)$,否则选择$(x+1, y)$:
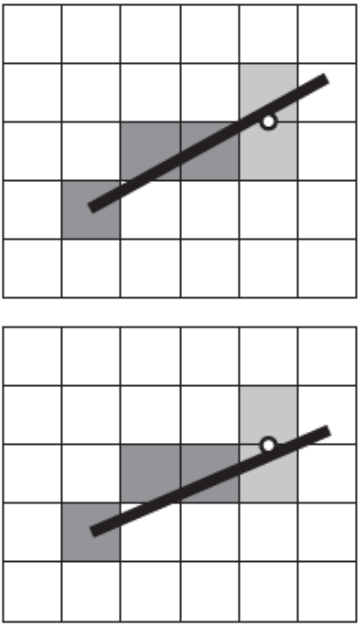
通过查看$f(x+1, y+0.5)$的正负性可以得知中点在直线的哪一方。如果=0说明中点在直线上,但是>0和<0并不能保证点位于直线的哪一方。
但是我们知道$x_1 − x_0>0$,所以在直线方程中y的系数一定是正的。所以如果y增加(正的变大,负的变小),整个函数的值就会增加。那么考虑极限情况$f(x, +∞)$,这时点$(x, +∞)$肯定在直线上方,而这时函数值一定是正的,那么我们就能确定:$f(x, y) > 0$,说明$(x, y)$位于直线的上方。
至此,上述的判断条件就可以是:
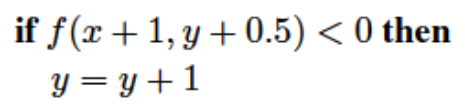
这是针对$m ∈ (0, 1]$的情况,对应比较扁平的直线(x增长比y快)。对于$m ∈ ( − 1, 0]$的情况一样,只不过$y+1$要变为$y-1$。对于比较垂直的直线(y增长比x快),比如$m ∈ (1, + ∞)$和$m ∈ ( − ∞, − 1]$,就是从下往上绘制直线。(if针对的是比较少发生的情况,对于扁平直线,往右的概率比往上大,所以是从左往右绘制直线,将往上的情况放入if)
如果需要更高的计算性能,还可以对上述算法进行改进。当我们绘制到$(x, y)$时,我们需要知道$f(x + 1, y + 0.5)$的值,但是这时我们已经知道$f(x, y + 0.5)$(当前这个点是被当成右边的点被选中)或者$f(x, y − 0.5)$(当前这个点是被当成右上的点被选中)的值,同时我们也知道:
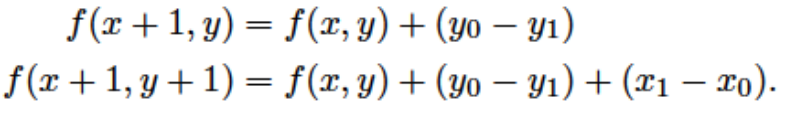
所以这时候我们不需要重新计算$f(x + 1, y + 0.5)$,只需要在第一个迭代时计算函数值,在后面的迭代中只需要往以前计算的函数值中加进$(y0 − y1)$或者$(y0 − y1) + (x1 − x0)$:
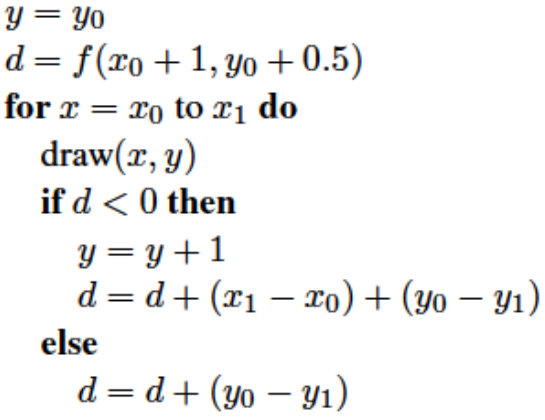
这是一个更快的方法,但是也许会累积错误。(比如$f(x, y + 0.5)$可能由许多长行相加组成),然而考虑到线条很少超过几千像素,所以这种错误不会是严重的。
如果将$(x1 − x0) + (y1 − y0)$和$(y1 − y0)$作为变量存储,计算还会更快。