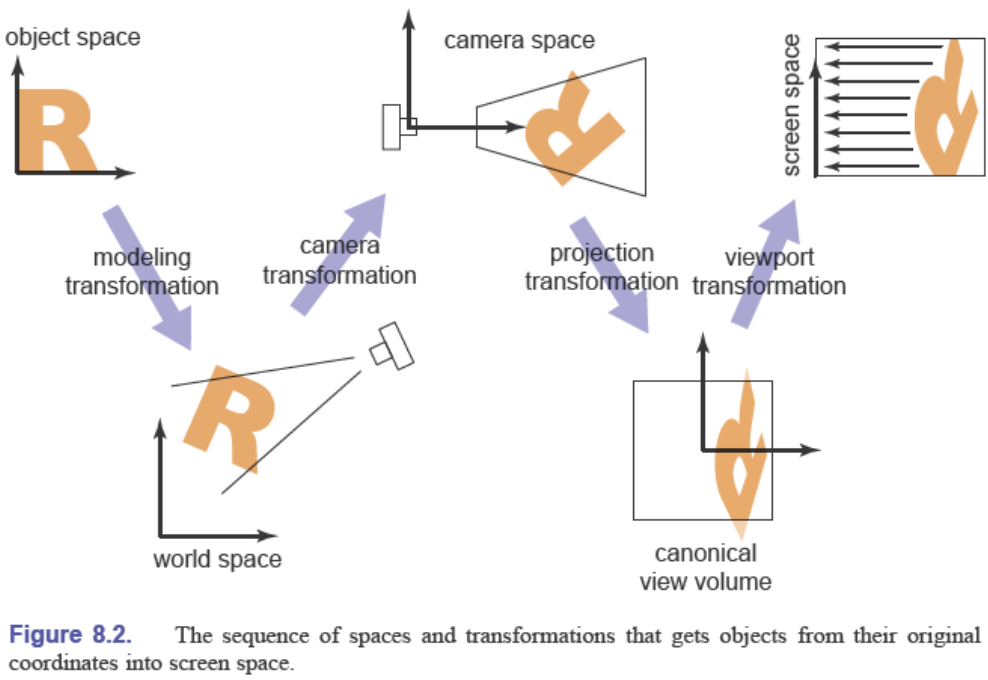
The 3D to 2D mapping is called a viewing transformation, and it plays an important role in object-order rendering, in which we need to rapidly find the image-space location of each object in the scene.

像第四章ray tracing中是将射线从图像平面中延申出去到3D场景中，view transformation则是将3D场景中的点映射到2D图像平面上，是上述过程的逆过程。但是这种映射并不包含遮挡的处理。

1 Viewing Transformations

View Transformations的任务就是将3D空间中的**$(x, y, z)$坐标转换为图像平面中的像素坐标**。

这是一个复杂的任务，但是可以将其分解为几个相对简单的阶段：

• camera transformations(eye transformations)：这是一种刚体变换。只要摄像机与场景物体的相对位置不改变，我们从摄像机中看到的图像就是一样的。所以为了方便后续的处理，将摄像机移动到原点，并将摄像机的朝向面向 $− z$的方向。场景中其他物体也跟随摄像机做相应的变换（相当于坐标系的变换）。这个变换只跟摄像机原始的位置和朝向有关。
• projection transformation：每个相机都有一个视野，包括平行投影相机和透视投影相机（平行投影相机视野是一个立方体，透视投影相机视野是一个棱台）。这次变换是将位于相机视野内的所有物体映射到$x∈( − 1, 1), y∈( − 1, 1), z∈( − 1, 1)$的立方体内。这个变换只跟投影类型有关。
• viewport transformation(window transformation)：这个变换将单位坐标映射到设备标准化的坐标。$[x∈( − 1, 1), y∈( − 1, 1)] ↦ [x∈(0, w), y∈(0, h)]$。$w, h$是设备分辨率。

$world \; space\xrightarrow[]{①}camera \; space\xrightarrow[]{②}canonical \; view \; volume\xrightarrow[]{③}screen\; space$

1.1 The Viewport Transformation

视口变换是将经过上一步操作后的立方体$( − 1, 1)^3$变换到以图像像素为基准的长方体$(0, w) × (0, h) × ( − 1, 1)$上，同时将坐标原点从中心移动至左下角。

we project x=-1 to the left side of the screen, x=+1 to the right side of the screen, y=-1 to the bottom of the screen, and y=+1 to the top of the screen.

实际上像素并不是一个点，而是一小块单位正方形区域。一个有$(n_x, n_y)$像素的点实际包含的区域是$[ − 0.5, n_x − 0.5] × [ − 0.5, n_y − 0.5]$。所以变换矩阵可以表达为：

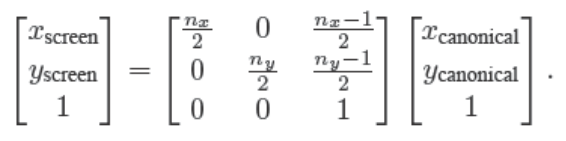
由于view transformation并没有对z轴做变换，所以上述公式里并未出现z轴。但是在实际应用中，还是需要将z轴加上。这将在遮挡处理上起作用：

1.2 The Orthographic Projection Transformation